Bijective functions applied to database operations

As part of my software development internship, I was given the task of automating the synchronization process between multiple schema-like databases from different deployment environments. We used Moodle LMS to create websites for our clients. Then we needed a tool to simulate the usual continuous deployment workflow we've been using for all other projects.

Indeed, Moodle works differently than any other software project, since the entire website is dynamically generated from a database at run-time - even HTML and CSS changes.

As a result, DevOps tools such as Jenkins and git are unlikely to be used. Knowing that many databases may have similar primary keys and cause rows to overwrite one another, a simple database synchronization could result in data loss.

It was, therefore, necessary to get work done. In 3 months, I had to create a tool that automates a task that is even nearly impossible to complete manually.

Prerequisites

The reader must have an understanding of the followings in order to follow along :

What are version control systems, especially git
What is git branching
What is continuous deployment
Basic knowledge of relational database model

Understanding the problem

Similar to git branches, we would like to merge multiple database content into a single one. There would be a production database and a number of development databases, which would be comparable to the main branch and the feature branches in git, respectively.

However, there is one catch, merge conflicts for databases are irreversible and result in data loss. There is no such thing as a Ctrl + Z shortcut to rollback database transactions, nor a magical emacs plugin to resolve row conflicts.

While I could have implemented such functionality, it would have taken me years and since we are smart people, we don't want to break with tradition of being lazy :). Thus I opted for a better solution.

Proposal

Initially, we could think of modifying the primary key value for each row in every database and referencing those changes through the forwarding keys. However, conflicts occur when more than one database is writing to the same row in a single table. The obvious solution is then to prevent such things from happening. Having databases write only on row numbers they should for merging would help avoid overlaps. Plus, Moodle does not have any referencing foreign keys.

Solution

Redefine the auto-increment behavior to allow for key pairing.

Two databases

Let's say we have 2 databases $A$ and $B$ . On one hand, we can manage to set the primary key value of $A$ to only odd numbers and make $B$ fill out the space for even values.

Hence, the value of a key $m$ is defined by its row number $n$ associated with the parity $p$ given to the specific database.

m = \lang n,p \rang = \begin{cases} 2n &\text{for odds } \\ 2n + 1 &\text{otherwise } \end{cases}

The broader case

We just need to find a bijection which associates to the unique value $m$ a pair of numbers $n$ and $q$ such that $q$ is a unique identifier of each database instead of its parity. We propose here to use the Cantor pairing function :

\pi : \N \times \N \implies \N

defined by

\pi \lparen n,q \rparen = \frac{\lparen n + q + 1 \rparen \lparen n + q \rparen}{2} + q

This function is even scalable because it can be inductively generalized to the Cantor tuple function :

\pi^{(n)} : \N^{n} \implies \N \medspace for \medspace n \gt 2

\pi^{(n)} \lparen k_1,\dots,k_{n-1},k_n \rparen \coloneqq \newline \\ \pi \lparen \pi^{(n-1)} \lparen k_1, \dots, k_{n-1} \rparen , k_n \rparen

which takes much more parameters into considerations.

We choose to use database triggers to apply this function before any row insertion for all databases to merge together. This is a simple database trigger example that would do the work (Not functional but massively simplified for clarity) :

CREATE TRIGGER IF NOT EXISTS `cantor_pairing_{$this->table}`
-- The pairing function is executed before every insert query for each table
BEFORE INSERT
ON `{$this->table}` FOR EACH ROW
BEGIN
    DECLARE q INT;
    DECLARE m INT;
    DECLARE n INT;

    -- Retrieves the database unique identifier
    SET q = (SELECT `server_id` FROM `dbsync_confg`);
    -- Retrieves the row insert number order
    SET n = (SELECT `value` FROM `next_insert_id` WHERE `table_name` = `{$this->table}`);
    -- Applies the Cantor pairing function
    SET m = (SELECT (((n + q + 1) * (n + q)) / 2) + q);
    -- Overrides the auto-increment value with m
    SET NEW.id = m;
END

Result

This graph speaks for itself. (Sorry for the contrast in dark mode :))

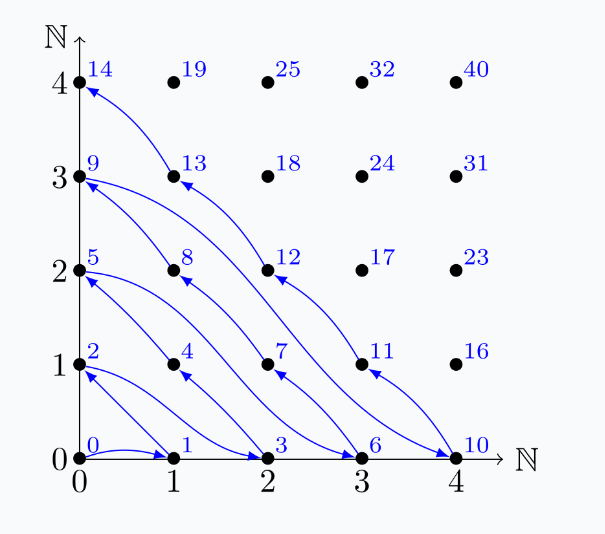
(Image Reference: By Florent Demesley at French Wikipedia, Creative Commons Attribution-Share Alike 3.0 Unported, this link)

The $x$ -axis represents the primary keys whereas the $y$ -axis represents the unique database identifier whereas the dots represent their primary key values.

Conclusion

It's hard to imagine that I went through this lot of math to get my bachelor's degree. It is even harder to think about how my superiors just waited for me to fail my internship as they gave me this task they can't even solve themselves. I don't even know how I managed to tackle the issue.

But if there's something I know is that I don't know nothing.

Indeed, Socrate :).

This article explains the importance of problem solving skills and why software developers must know the under the hood of how things work if you want to stand out from others. No one knows where math can lead us, no one knows its limits and the benefits it can bring to humanity. But from now, Artificial Intelligence is where it shines. Everyone should keep an eye on it like I do as I am preparing to write an article on AI sooner or later so stay tuned.